傅里叶级数展开公式如下:
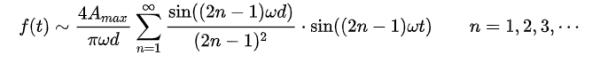
傅里叶级数像三角波,来自矩形波,梯形波这种波形不连续,因此在仿真软件中很容易出现计算不收敛的情况。所以,在这种帮护养攻情况下,利用一系列谐波叠加的形式来等价于原来的波形,可以很好的优化模型。
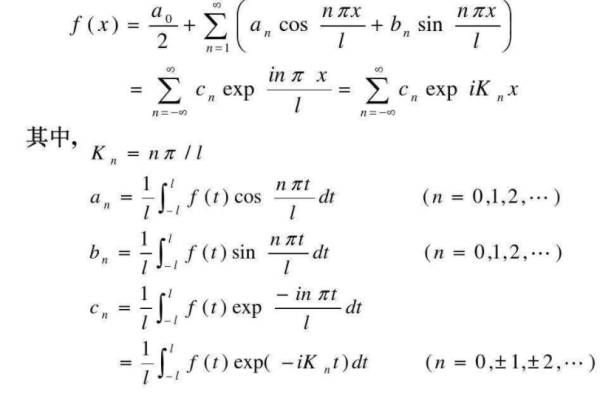
傅里叶展开式收敛性判别
至今还没有判断傅里叶级数的收敛性充分必要条件,但是对于实际问题并让中出现的函数,有很多种判别条件可用于判断收敛性。闹大比如x(t)的可微性或级数的一致收敛性。
在闭区间上满足探境狄利克雷条件的函五数表示成的傅里叶级数都收敛。狄利克雷条件如下:在定义区间上,x(t)须绝对可积;在任一有液蔽竖限区间中,x(t)只能取有限个极值点;在任何有限区间上,x(t)只能有有限个第一类间断点。
以上资料参考:百度百科-傅里叶展开式