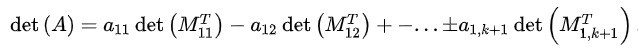求矩阵的行列式,如果矩阵的的阶数小于3,可以利用对角线法则计算矩阵的行列式,如果大于三阶可以化为三角矩阵,三角矩阵的行列式为对角线元素的乘积。
一个n×n矩阵的行列式等于其任消御意行(或列)的元素与对应的代数余子式乘积之纳段和。
可以利用矩阵的性质,进行矩阵的洞桥誉化简。矩阵初等变换不改变矩阵的行列式。
扩展资料:
矩阵行列式的基本定理:
1、设A为一n×n矩阵,则det(A转置)=det(A)。
证 对n采用数学归纳法证明。显然,因为1×1矩阵是对称的,该结论对n=1是成立的。假设这个结论对所有k×k矩阵也是成立的,对(k+1)×(k+1)矩阵A,将det(A)按照A的第一行展开,我们有:
det(A)=a11det(M11)-a12det(M12)+-…±a1,k+1det(M1,k+1)。
由于Mij均为k×k矩阵,由归纳假设有
2、设A为一n×n三角形矩阵。则A的行列式等于A的对角元素的乘积。
根据定理1,只需证明结论对下三角形矩阵成立。利用余子式展开和对n的归纳法,容易证明这个结论。
3、令A为n×n矩阵。
若A有一行或一列包含的元素全为零,则det(A)=0。
若A有两行或两列相等,则det(A)=0。这些结论容易利用余子式展开加以证明。