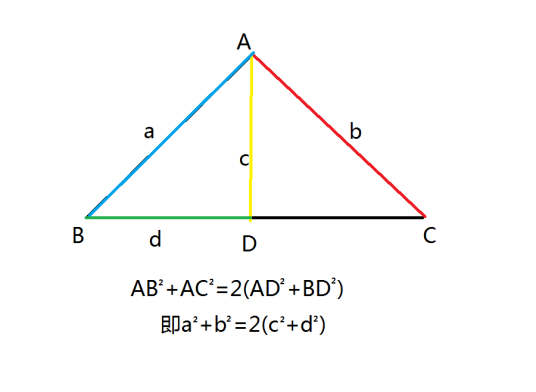
三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:
1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG︰答迟GH=1︰2。(此直线称为三角形的欧拉线(Euler line))
3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
4、垂心分每条高线的两部分乘积相等。
定理证明
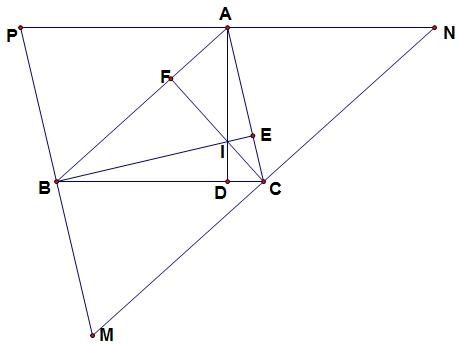
已知:ΔABC中,AD、BE是两条高,AD、BE相交于点O,连接CO并延长交AB于点F ,求清闹李证:CF⊥AB
证明:
连接DE ∵∠ADB=∠AEB=90度 ∴A、B、D、E四点共圆 ∴∠ADE=∠ABE
∵∠EAO=∠DAC ∠AEO=∠ADC ∴ΔAEO∽ΔADC
∴AE/AO=AD/AC ∴ΔEAD∽ΔOAC ∴∠弯猜ACF=∠ADE=∠ABE
又∵∠ABE+∠BAC=90度 ∴∠ACF+∠BAC=90度 ∴CF⊥AB
因此,垂心定理成立!