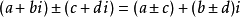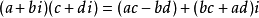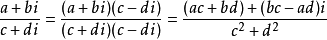Simone复数是形如 a ＋ b i的数。式中a，b 为 实数，i是一个满足i^2 ＝－1的数，因为任何实数的平方不等于－1，所以i不是实数，而是实数以外的新的数。
在复数a＋bi中，a称为复数的实部，b称为复数的虚部，i称为虚数单位。当虚部等于零时，这个复数就改备侍是实数；当虚部不等于零时，这个复数称为虚数，虚数的实部如果等于零，则称为纯虚数。由上可知，复数集包含了实数集，因而是实数集的扩张。
复数有多种表示形式，常用形式 z ＝ a ＋ b i叫做代数式。此外有下列形式。
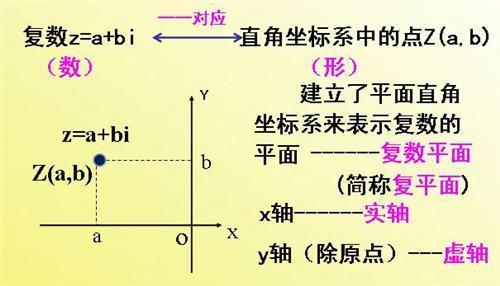
①几何形式。复数 z ＝ a ＋ b i 用直角坐标平面上点 Z （ a ， b ）表示。这种形式使复数的问题可以借助图形来研究。也可反过来用复数的理论解决一些几何问题。
②向量形式。复数 z ＝ a ＋ b i用一个以原点 O 为起点，点 Z （ a ， b ）为终点的向量 O Z 表示。这种形式使复数的加、减法运算得到恰当的几何解释。
③三角形式。复数 z＝ a ＋ b i化为三角形式
z ＝｜滚喊 z ｜（cos θ ＋isin θ ） 式中｜ z ｜= ，叫做复数的模（或绝对值）； θ 是以 x 轴为始边；向量 O Z 为终边的角，叫做复数的辐角。这种形式便于作复数的乘、除、乘方、开方运算。
④指数形式。将复数的三角形式 z ＝｜ z ｜(cos θ ＋isin θ ）中的cos θ ＋isin θ 换为 e i q ，复数就表为指数形式
z ＝｜ z ｜ e i q ， 复数的乘、除、乘方、开方可以按照幂的运算法则进行。
复数集不同于实数集的几个特点是：开方运算永远可行；一元 n 次复系数方程总有 n 个根（重根按重数计）；复数不能建立大小顺序。
扩展资料：
根据定义，若 
(a，b∈R），则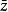 
=a－bi（a,b∈R）。共轭复数所对应的点关于实轴对称。两个复数：x+yi与x-yi称为共轭复数，它们的实部相等，虚部互为相反数。
在复平面上，表示两个共轭复数的点关于X轴对称，而这一点正是"共轭"一词的来源----两头牛平行地拉一部犁，它们的肩膀上要共架一个横梁，这横梁就叫做"轭"。如果用z表示x+yi，那么在z字上面加个"一"就表示x-yi，或相反。
1 加法法则
复数的加法法则：设z1=a+bi，z2=c+di是任意两个复数。两者和的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。两个复数的和依然是复数。
即 
2 乘法法则
复数的乘法法则：把两个复数相乘，类似两个多项式相乘，结果中i2= -1，把实部与虚部分别合并。两个复数的积仍然是一个复数。
即 
3 除法法则
复数除法定义：满足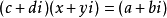 
的复数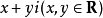 
叫复数a+bi除以复数c+di的商。
运算方法：将分子和分母同时乘以分母的共轭复数，再用乘法法则运算，
即 
4 开方法则
若zn=r(cosθ+isinθ），则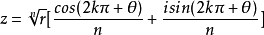
（k=0，1，2，核吵3…n-1）
我们把数学分析中基本的实变初等函数推广到复变初等函数，使得定义的各种复变初等函数，当z变为实变数x(y=0）时与相应的实变初等函数相同。
注意根据这些定义，在z为任意复变数时，
①．哪些相应的实变初等函数的性质被保留下来
②．哪些相应的实变初等函数的性质不再成立
③．出现了哪些相应的实变初等函数所没有的新的性质。
复数运算法则有：加减法、乘除法。两个复数的和依然是复数，它的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。复数的加法满足交换律和结合律。此外，复数作为幂和对数的底数、指数、真数时，其运算规则可由欧拉公式e^iθ=cos θ+i sin θ（弧度制）推导而得。
加法法则
复数的加法按照以下规定的法则进行：设z1=a+bi，z2=c+di是任意两个复数，
则它们的和是 (a+bi)+(c+di)=(a+c)+(b+d)i。
两个复数的和依然是复数，它的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。
复数的加法满足交换律和结合律，
即对任意复数z1，z2，z3，有： z1+z2=z2+z1；(z1+z2)+z3=z1+(z2+z3)。
减法法则
复数的减法按照以下规定的法则进行：设z1=a+bi，z2=c+di是任意两个复数，
则它们的差是 (a+bi)-(c+di)=(a-c)+(b-d)i。
两个复数的差依然是复数，它的实部是原来两个复数实部的差，它的虚部是原来两个虚部的差。
参考资料：百度百科-复数
