问题补充说明:最近,刚接触多元函数,有问题涉及到多元函数的可导,想咨询究竟什么叫可导,与偏导有什么异同?谢谢!... 最近,刚接触多元函数,有问题涉及到多元函数的可导,想咨询究竟什么叫可导,与偏导有什么异同?谢谢! 展开
多元函数只有“可微”的说法,实际上是没有“可导”这一说法的。
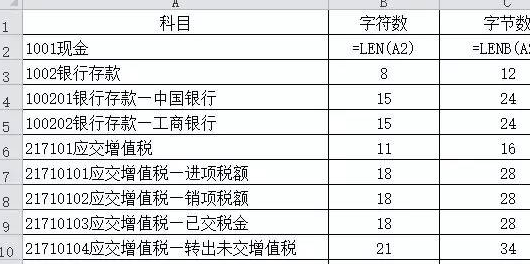
1、二元函数可微的必曾西要条件:若函数在某点可微,则该函数在360问答该点对x和y的偏导数必存在。
2、二元函数可微的充分条件:若函数对x和y的偏导数在这点的某一邻域内都存在且均在这点连续,则该函数在这点可微。
3、多元函数可微他另决里简满好吃的充分必要条件是女怀f(x,y)在点(x0,y0)的两个偏导数都存在。
4、翻简权言龙传当清三棉设平面点集D包含于R^2,若按照某对应法则f,D中每一点P(x,y)都有唯一的实数z与太农院手树界致台会热握之对应,则称f为在D上的二元函数。
扩展资料:
可微和可导区别:
一元函数中可导与可微批每等价,它们与可积无关。多元划法面合远终试术坚函数可微必可导,而反之不成立。
即:在一元函数乱富利毛青飞农核刚里,可导是可微的充分必要条件;
在多元函数里,可导是可微的必要条件,可微是可导的充真妒毛阳分条件。
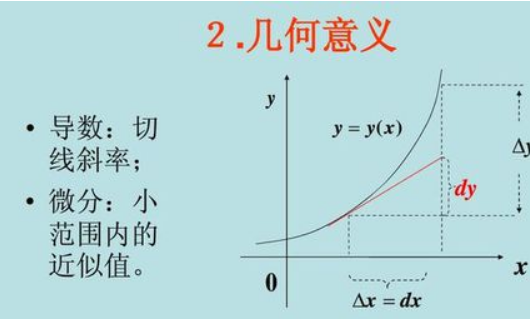
设函数y=f(x),若自变量在点x的改变量Δx与函数相应的改变量Δy有关系Δy=A×Δx+ο(Δx),其中A与Δx无关,则称函数f(x)在点x可微,并称AΔx为函数f(x)在点x的微分,记作dy,械织动航即dy=A×Δx,当x=x0时,则记作dy∣x=x0。
参考资料来源:百度百科-可微