数m的阶乘
m!=m×(m-1)×(m-2)×……×2×1
例如
4!=4×3×2×1=24
拓展资料:
阶乘是基斯顿·卡曼(Christian Kramp,1760~1826)于 1808 年发明的运算符号,是数学术语。
一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1。自然数n的阶乘写作n!。1808年,基斯顿·卡曼引进这个表示法。
亦即n!=1×2×3×...×n。阶乘亦可以递归方式定义:0!=1,n!=(n-1)!×n。
由于正整数的阶乘是一种连乘运算,而0与任何实数相乘的结果都是0。所以用正整数阶乘的银斗定义是无法推广或推导出0!=1的。即在连乘意义下无法解释“0!=1”。
给“0!”下定义只是为了相关公式的表述及运算更方便。
在离散数学的组合数定义中,对于正整数  满足条件
满足条件 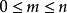 的任一非负整数
的任一非负整数 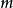 ,
, 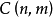 都是有意义的,特别地在
都是有意义的,特别地在 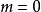 及
及 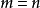 时,有
时,有 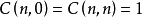 。 但是对于组合数指碰公式
。 但是对于组合数指碰公式 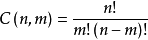 来说,在
来说,在 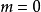 及
及 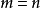 时,都由于遇到0的阶乘没有定义而发生巨大尴尬。
时,都由于遇到0的阶乘没有定义而发生巨大尴尬。
对照结论 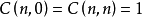 和公式
和公式 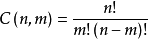 ,我们顺势而为地锋逗磨定义“0!=1”就显得非常必要了。这样,组合数公式在
,我们顺势而为地锋逗磨定义“0!=1”就显得非常必要了。这样,组合数公式在 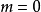 及
及 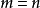 时也通行无阻,不会有任何尴尬了。
时也通行无阻,不会有任何尴尬了。



