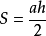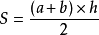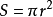Simone长方形(矩形）： S=ab{长方形面积=长×宽}
正方形：S=a^2 {正方形面积=边长×边长}
平行四边形：S=ab {平行四边形面积=底×高}
三角形： 
{三角形面积=底×高÷2}
梯形： 
{梯形面积=（上底+下底）×高÷2}
圆形（正圆）： 
{圆形（正圆）面积=圆周率×半径×半径}
圆环：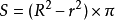 
{圆形（外环）面积={圆周率枝贺×（外环半径^2-内环半径^2）}
扇形：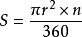 
{圆形（扇形）面积=圆周率×半径×半径×扇形角度/360}
长方体表面积：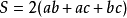 
{长方体表面积=（长×宽+长×高+宽×高）×2}
椭圆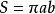 
(其中π(圆周率，a,b分别是椭圆的长半轴，短半轴的长).
扩展资料
面积是表示平面中二维图形或形状或平面层的程度的数量。表面积是三维物体的二维表面上的模拟物。面积可以理解为具有给定厚度的材料的量，面积是形成形状的模型所必需的，或者用单一涂层覆盖表面所需的涂料量。它是曲线长度（一维概念）或实体体积（三维概念含搭衡）的二维模拟。
有几种众所周知的简单形状的公式，如三角形，矩形和圆形。使用这些公式，可以通过将多边形分成三角形来找到任何多边形的面积。对于具有弯曲边界的形状，通常需要谈做微积分来计算面积。事实上，确定飞机数字面积的问题是演算历史发展的主要动机。
对于诸如球体，锥体或圆柱体的实体形状，其边界面的面积被称为表面积，简单形状的表面区域的公式由古希腊人计算，但计算更复杂形状的表面积通常需要多变量微积分。
参考资料百度百科-面积
