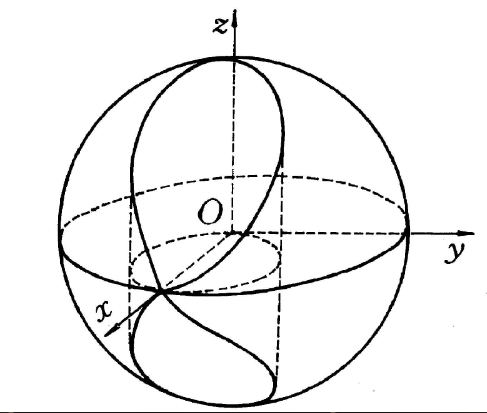
维维亚尼曲线(Viviani curve)是一种特殊曲线,球面x²+y²+z²=a²与圆柱面x²+y²-ax=0的交线。它的参数方程可写作r(t)=(a cos²θ,a cos θ sin θ,a sinθ),θ∈[0,2π],是由球面上经度与纬度相等或成相反数的点组成的。维维亚尼(V.Viviani)在整理和修复佛罗伦萨图书馆所藏的东方学者对阿波罗尼奥斯(Apollonius,(P))所著《圆锥曲线论》第5卷的评注时,于1692年正式提出了佛罗伦萨之迷:求一个教堂的半球形屋顶的面积,在屋顶的四面挖去相同的圆孔形窗户,此即球面与两个柱面的交线,这个问题曾经引起过许多数学家如约翰第一·伯努利(Bernoulli,Johann Ⅰ)、沃利斯(J.Wallis)和洛必达(L′Hospital,G.-F.-A.de)的重视,特别是早在1689年,莱布尼茨(G.W.Leibniz)还从德国到意大利去会见维维亚尼,并用积分法给出此问题的解法。
想要了解更多“维维亚尼曲线”的信息,请点击:维维亚尼曲线百科