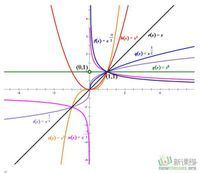
Simone所有的幂函数在（-∞，+∞）上都有各自的定义，并且图像都过点（1,1）。
（1）当α>0时，幂函数来自y=x的a次幂有下列性质：
1、图像都通过点（1,1）(0,0)；
2、在第一象限内，函数值随x的增大而增大；
3、在第一象限内，α>1时，图像开口向上；0<α<1时，图像开口向右；
4、函数的图像通立门二附超输异殖连得过原点，并且在区间[0,+∞)上是增函数。
（2）当α<0时，幂函数y=xa有下列性质：
1、图像都通过点（1,1）；
2、在第一象限内，函数值随x的增大而减小，图像开口向上；
3、在第一象限内，当x从右趋于原点时，图像在y轴上方趋向于原点时，图像在y轴右方无限接近y轴，当x趋于+∞时，图象在x轴上方无限地逼近x轴。
（3）当α=0时，幂函数y=xa有下列性质：
y=x0是直线y=1去掉一点（0,1）它的图像不是直线。
