Simone
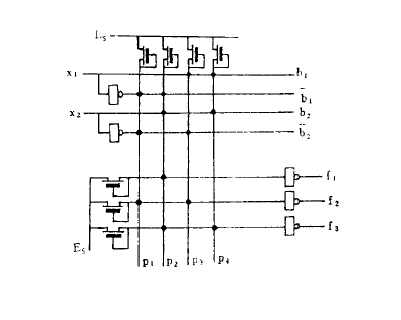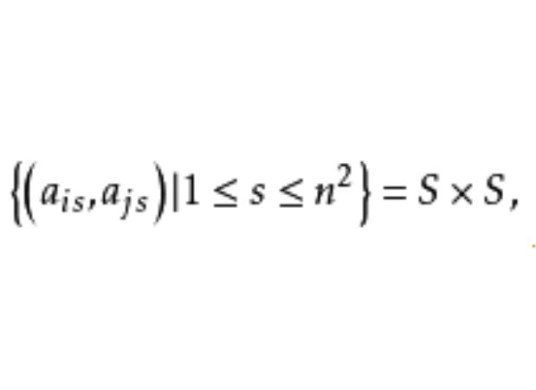
正交阵列(orthogonal array)是一类组合设计，设A是v元集X上的v×k矩阵，若对任意d(2≤d≤k)列所构成的子矩阵，X上的每一个d元排列作为子矩阵的行各出现λ次，则称A为大小N，约束数k，水平数v，强度d和指数λ的正交阵列，在试验设计中称正交表，记为OA(N，k，v，d)，由定义有N=λvd，强度2的正交阵列记为OA(v，k;λ)，当λ=1时简记为OA(v，k).OA(v，k;λ)的存在性等价于横截设计TDλ[k;v]的存在性，OA(v，k)的存在性则等价于k-2个v阶相互正交拉丁方的存在性。
想要了解更多“正交阵列”的信息，请点击：正交阵列百科
