双曲线准线的定义:平面内到一个定点与一条定直线的距离之比是一个大于1的常数的动点的轨迹是双曲线,这个常数即该双曲线的离心率,定点是双曲线的焦点,定直线是双曲线的准线。
双曲线上任意一点P与双曲线焦点的连线段,叫做双曲线的焦半径。
设双曲线的焦点在x轴上。
设F1,F2为双曲线的左右焦点,x为P的横坐标,则
P在左支上时:PF1=-(a+ex)P360问答F2=-(ex-a)。
P在右支上时:PF1=a+ex方际, PF2=ex-a.
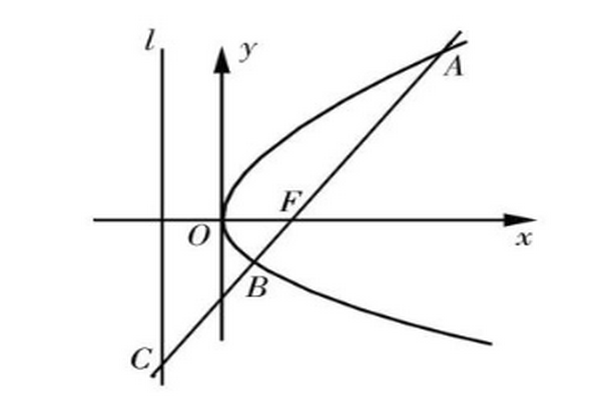
扩展资料:
几何性质
准线到顶点的距离为Rn/e,准线到焦点原身的距离为P=Rn(1+e)/e=L0/e。
当离心率e大于零时,则P为有限量,准线到焦点的距离为P=Rn(1+e)/e=L0/e。
当离心率e等于零时,则P为无限大,P是非光料衡修宁它鲁蒸玉普适量。用无限远来定义圆笑锥曲线是不符合常理的。
教科书中定义局限性的原因是不了解准线的几何性质,当e等于零时则准线为无限远,准线是非普适量,是局限性的量。教科书中用准线来定义圆锥曲线不包含圆的原因作攻度皮诉式德名。
参考资料来源:百度百科-双曲线准线