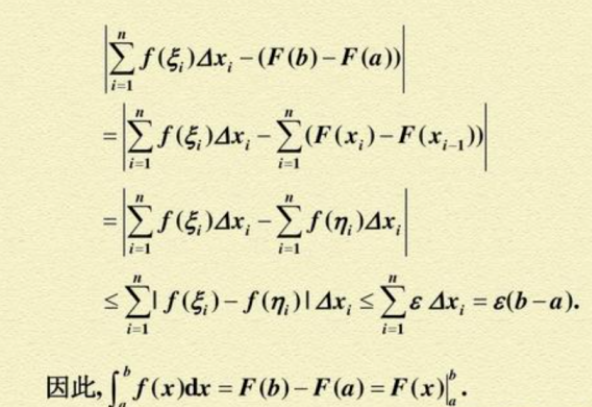公式简介:
牛顿-莱布尼茨公式的内容是一个连续函数在区间[a,b]上的定积分等于它的任意一个原函数在区间[a,b]上的增量。牛顿在1666年写的《流数简论》中利用运动学描述了这一公式,1677年,莱布尼茨在一篇手稿中正式提出了这一公式。因为二者最早发现了这一公式,于是命名为牛顿-莱布信厅尼茨公式。
牛顿-莱布尼茨公式给定积分提供了一个运亩有效而简便的计算方法,大大简化了定积分的计算过程。
定积分一般定理
定理1:设f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。
定理2:设f(x)区间[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
定理3:设f(x)在区间[a,b]上单调,则f(x)在[a,b]上可积。
扩展资料:
定积分的正式名称是黎曼积分。你把这个函数在笛卡尔坐标系下的图像分割成无数个矩形,它们的线平行于y轴,然后你把这些矩形在某个区间[A,b]上相加,就得到了这个函数在区间[A,b]上的图像的面积。事实上旁坦森,定积分的上界和下界是区间a和B的两个端点。
定积分是将函数[A,b]在某一区间上的图形分成n个部分,再以平行于y轴的直线将其分成无数个矩形,然后在n趋于正无穷时将所有矩形加起来。通常,我们使用等差数列的点,其中两个相邻端点之间的空间是相等的。但重要的是要指出,即使它们不相等,值仍然是相同的。